Syzygy Analytics

Introduction

In this article I am going to consider the topic of fixture adjusting.  All fans will know that teams are likely to perform better against opposition that is ranked lower in the table and vice versa.  This blog is all about the predictive and we don’t want our ratings of a team to be skewed by their opposition.  If we are going to have a predictive rating we want to have an accurate measure of the teams’ intrinsic level so we need to remove as much ‘noise’ as possible.

I will always be using team ratings in the style of in the style of a performance delta per game.  E.g. if the home team has 10 shots in a game and the away team has 5, the home teams rating for that game is +5.  If a team has 6.25 xG for and 10.1 xG against over 5 games then the team’s rating for that sample of games is -0.77 (xG).

How to apply a fixture adjustment

Let’s make a mock 10 team league and assume the ability of each team is as follows:

Let’s consider an example:

Say a league average¹ team (Team D here) starts the season playing teams A and C (one home and one away so it balances out) – we’d expect their rating after 2 games to be around -1.2 – both opponents are better than them to the tune of about 1.2 xG per game. 

We ‘know’ Team D’s ability is really 0 though (average).  We want their rating to show as 0 otherwise we are not rating their true ability correctly.  This all means our fixture adjustment for team D after 2 games is going to be +1.2. 

Considering a different example,Team B plays teams F and I, one home and one away.  Again we consider the performance of an average team and conclude the fixture adjustment for Team B will be -0.6. 

Seems simple enough but I believe the 2^nd example is currently wrong.  It’s not way off but there’s something missing – can you spot it?

Special Adjustment

Let’s play out a whole season in this mock league and calculate the fixture adjustment of each team.  The results are as follows

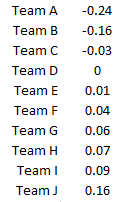
After the whole season it appears that we still have various adjustments to make.  Team A loses 0.24 off their team performance because a league average team would expect to average a performance of +0.24 with Team A’s entire schedule.

This can’t be right – no one would say a league is unfair as some teams have an easier schedule than others.  Why should a good team forever be punished by fixture adjustment?  Their opponents are only ‘bad’ because the good team has made them look that way.

This happens because this method so far results in the fixture adjustment being a function of the teams own ability.  From Team A’s perspective the average team in the league has a below average rating of -0.24.  We don’t want our schedule adjustment to be affected by the ability of the team we are adjusting for, we want it to depend on the ability of their opponents.

The adjustment we require is quite simple – to make it so every team faces an average schedule we add a factor of

(Team Rating) / (total teams in the league – 1)

where Team Rating is the rating of the team we are calculating the schedule adjustment for.

In example a) above the factor is zero as team rating is 0 in that case.  Using the formula for example b) we calculate 1.4 / 9 = 0.16.  This means we add a factor of 0.16 to the team rating of all the teams that Team B plays.  This means the fixture adjustment for team B would be -0.44 after playing team F and team I.

The fixture adjustment of each team once the league is finished would now be zero – exactly what we want.

I would define a fixture adjustment for any Team ‘X’ as ‘the performance of a league average side against Team X’s opponents in an otherwise similar league without Team X’.

Circular Issues

In order to calculate the fixture adjustment we need the true performance level of the opponents.  The method is somewhat counterintuitive because we are trying to calculate the true performance level of every team but we need the performance levels of the teams as an input to adjust for schedule.  With smaller samples I recommend estimating the level of each opponent rather than inputting their raw performance.  If the adjusted ratings significantly change your estimated ratings it would be reasonable to recalculate the schedule adjustment with the new ratings.

Summary

We now have a complete adjustment to add to the rating of a team.  For Team A this is

Fixture adjusted rating  =

raw rating + Average level of Team A’s opponents + (rating of Team A / (total league teams – 1))

Remember this applies when the team rating is in the format of +3 shots per game or +0.5 xG per game or +1 goal per game e.t.c

Quiz

Calculate the fixture adjusted rating for the following team.

The team in question have a rating of +0.3 xG after 5 games and they have played teams we estimate are of levels -0.1 xG, -0.05 xG, +0.2 xG, +0.5 xG, and +1.0 xG in a 20 team league. 

Answer (select to see) = +0.626 xG (3 decimal places)#

If you would like to get in touch about anything you can e-mail syzygy112358@proton.me or tweet me at https://x.com/SamH112358

Glossary

1 It’s interesting to note there could be different definitions of ‘league average’.  In this case average to us means total attacking output is equal to the total attacking output of their opponents (i.e. their goal difference equals 0).  However it’s also not unreasonable to argue that the average side is the middle team of the league, e.g. 10^th in a 20-team league.  If a league is skewed towards either having some very dominant teams or very weak teams then the middle team (10^th in a 20 team league) would not be expected to have a goal difference of zero.  For all analytical purposes our ‘league average’ team is going to be the one with a goal difference of zero, an xG difference of zero, a shot ratio of 0.5 e.t.c.